3. 불확도의 표현

 

3-1. 단일측정에서의 불확도 표현

 

불확도=최소눈금/2

예1: 최소눈금 1mm인 자로 길이 측정

불확도=0.5

 100원 동전 지름=24.0±1mm

(눈금을 읽을 때의 불확도가 양쪽 끝에서  각각 0.5mm로 판단된 경우, 오른쪽 값에서 왼쪽 값을 빼야하므로 뒤에 설명할 오차의 전파공식을 써서 불확도를 계산한다.)

불확도는 다음과 같이 조건에 따라 최소눈금보다 크거나 작아질 수도 있다.

 탁구공 지름=37±4mm

(눈금을 읽을 때의 불확도가 양쪽 끝에서 각각 2mm로 판단된 경우)

 

 

 

예2: 디지털 저울로 물체의 질량 측정

 

 

 물체의 질량=23.7±0.1g

( 측정할 때 최소 눈금에 의한 불확도 0.05g, 영점을 읽을 때 최소 눈금에 의한 불확도 0.05g)

* 이와 같이 최소눈금으로부터 직관적으로 불확도를 추정할 경우 최소눈금보다 더 낮은 자리수의 측정값에 대한 정보가 전혀 없으므로 추정한 불확도의 2배 폭을 가진 직사각형의 확률분포를 가정할 수 있다. 이 때 표준편차를 계산하면 불확도/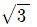 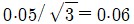3√ 이 되므로 위에서 예로 든 디지털 저울의 경우 더 정확한 불확도는  이 된다.

 

 

3-2. 반복측정에서의 통계적인 불확도 표현

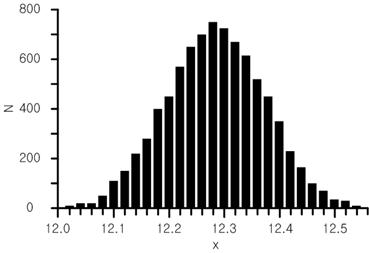
•  측정값: x1

 

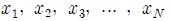
• 평균(average, mean): 참값의 최적추정값

 

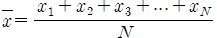
• 편차

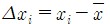
• 표준편차(standard deviation): 측정값들이 평균값을 중심으로 흩어진 정도를 나타냄. 측정횟수가 증가해도 크게 변하지 않음.

 

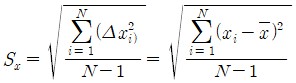
• 표준오차(standard error): 평균값들로 구성된 분포의 표준편차.  평균값에 대한 불확도를 나타낸다. 측정횟수가 증가할수록 감소한다.

 

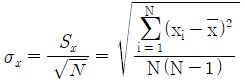
  * 측정횟수가 무한대이면 표준오차가 0이 된다는데 주목하자. 그리고 평균값을 한 번만 측정하여 평균값의 표준편차를 추정한다는데 주목하자.

• 반복 측정의 결과는 다음과 같이 보고 한다.

 

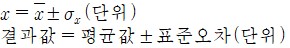
예: 초시계(최소단위 0.001초)를 사용하여 진자의 주기를 측정

 측정값

x1=2.45s

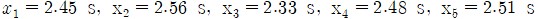
  평균

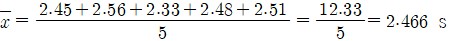
 표준편차

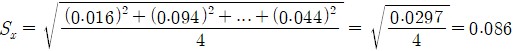
 표준오차

 

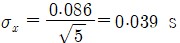
진자의 주기  

 

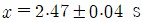
3-3. 두 가지 이상의 불확도가 합성된 합성 불확도(Combined Uncertainty)

 

예: 

측정값=723.2 mm

 

불확도 1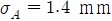  

 

불확도 2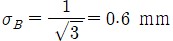  

 

두 불확도를 포함한 합성불확도를 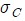 라 할 때 오차의 전파 공식을 사용하면

σC=σA2+σB2−−−−−−−−√=1.5mm

 

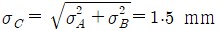
측정결과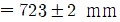

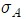*  와 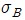  의 값 차이가 크면 (약 3 배 이상) 작은 쪽은 무시할 수 있다